Answer:
10th week
Explanation:
We have been given that
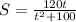
Now, we have to find t for S= 6
Substituting, the value of S in above equation
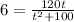
Cross multiplying, we get

Subtract 120t to both sides
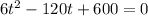
Divide both sides by 6
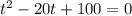
We can write this in perfect square as

Solve for t

Therefore, in 10th week, the sale would have been 6.