Answer:
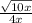
===========================================================
Work Shown:
The idea is to multiply top and bottom by sqrt(8x) to make the denominator rational (ie get rid of the square root)
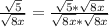
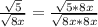
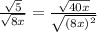
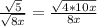
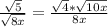
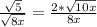
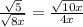
where x > 0 for each step shown above
note: refresh the page if the math symbols do not show up