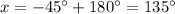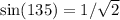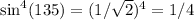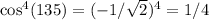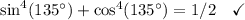I'll assume that what was meant was
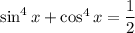
.
The exponent in the funny place is just an abbreviation:
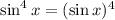
.
I hope that's what you meant. Let me know if I'm wrong.
Let's start from the old saw

Squaring both sides,

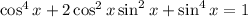
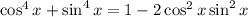
So now the original question
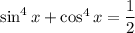
becomes

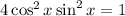
Now we use the sine double angle formula
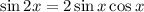
We square it to see
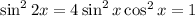
Taking the square root,
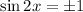
Not sure how you want it; we'll do it in degrees.
When we know the sine of an angle, there's usually two angles on the unit circle that have that sine. They're supplementary angles which add to
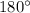
. But when the sine is 1 or -1 like it is here, we're looking at
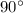
and
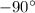
, which are essentially their own supplements, slightly less messy.
That means we have two equations:
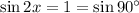
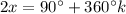
integer

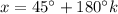
or
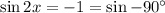
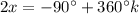
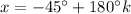
We can combine those for a final answer,
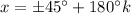
integer

Check. Let's just check one, how about