Question

the area of the rectangle is 54 M squared and the length of the rectangle is 3 meters more than twice the width. what is the length and the width?

Answer 1

We know that the area of a rectangle is solved via the equation:


`A=l*w`

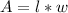
And we are told that the area of the rectangle is 54
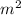
`m^(2)`, so:


`54 m^(2)=l*w`

We are told that the length is 3 meters more than twice the width, so we can then set up the equation:


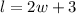
`l=2w+3`, with w representing the width of the rectangle

Let's plug the above equation into the equation representing area:


`54=(2w+3)*w`

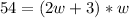
Simplify the right side:


`54=2 w^(2)+3w`

And then subtract 54 from both sides to set the equation equal to 0 for factoring purposes:


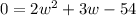
`0=2 w^(2)+3w-54`; then factor:


`0=(2w-9)(w+6)`

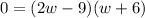
Set each term equal to 0, and solve for w. We get the answers:


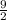
`(9)/(2)` and
`-6`

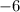
Since the width cannot be a negative number, we take the positive value as the true width. Now we know that the width is
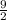
`(9)/(2)` meters.

Let's plug this value into the equation for the length:


`l=2w+3`

`l=2( (9)/(2))+3`

`l=9+3=12`

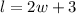
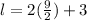
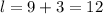
So now we know that the length is 12 meters.

Overall, the length of the rectangle is 12 meters and the width of the rectangle is
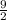`(9)/(2)` meters.