Answer: The required co-ordinates of vertex H' are (4, 2).
Step-by-step explanation: Given that the co-ordinates of trapezoid EFGH are E(4, 6), F(2, 3), G(4, 2), and H(8, 4) and its image EFGH under dilation is E'F'G'H'.
The co-ordinates of vertex G' are (2, 1).
We are to find the co-ordinates of vertex GH.
Let d denote the dilation factor of trapezoid EFGH to E'F'G'H'.
Then, according to the given information, we must have
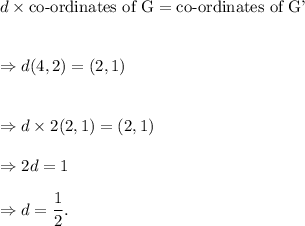
Therefore, the co-ordinates of vertex H' are given by
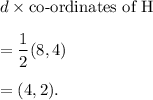
Thus, the required co-ordinates of vertex H' are (4, 2).