1.
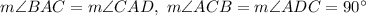 , then
, then
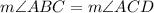 and triangles ADC and ACB are similar by AAA theorem.
and triangles ADC and ACB are similar by AAA theorem.
2. The ratio of the corresponding sides of similar triangles is constant, so
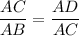 .
.
3. Knowing lengths you could state that
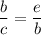 .
.
4. This ratio is equivalent to
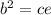 .
.
5.
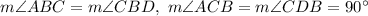 , then
, then
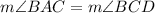 and triangles BDC and BCA are similar by AAA theorem.
and triangles BDC and BCA are similar by AAA theorem.
6. The ratio of the corresponding sides of similar triangles is constant, so
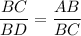 .
.
7. Knowing lengths you could state that
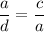 .
.
8. This ratio is equivalent to
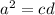 .
.
9. Now add results of parts 4 and 8:
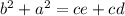 .
.
10. c is common factor, then:
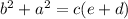 .
.
11. Since
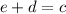 you have
you have
 .
.