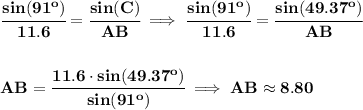Question

I need help with Q 5 and 6.

Answer 1

In fact, you have already started solving the problem using the sine rule, by the fact of drawing arrows.

We have an obtuse triangle, so there is no ambiguity using the sine rule to solve for R and Q, since they will both be acute.

(i) angle R
Using the sine rule,
sin(R)/13.4=sin(101)/20.8
=>
sin(R)=sin(101)/20.8*13.4=0.6434944
and
R=39.227 degrees, or R=39.2 degrees (to 1 decimal)

(ii) Angle Q
Using the sum of angles of a triangle,
angle Q = 180-(101-39.227)=39.773 degrees,
or angle Q=39.8 degrees to one decimal

(iii) Side PR

using cosine rule
PR^2=PQ^2+QR^2-2*PQ*QR*cos(Q)
=13.4^2+20.8^2-2(13.4)(20.8)(0.768585)
=170.56+432.64-428.4401
=183.7599
=>
PR=sqrt(183.7599)=13.5558 (to four places), or
PR=13.6 cm (to 1 decimal)

Using sine rule:
PR/sin(Q)=RQ/sin(P)
=>
PR=RQ*(sin(Q)/sin(P))
=20.8*sin(39.77)/sin(101)
=20.8*0.639748/0.981627
=13.556 or 13.6 cm (to one decimal)

Answer 2

check the top part of the picture below.

since we know that angle R is 39.23, then angle Q is just 180 - R - P, or about 39.77°.

and to get the length of PR,


`\bf \cfrac{sin(101^o)}{20.8}=\cfrac{sin(Q)}{PR}\implies \cfrac{sin(101^o)}{20.8}=\cfrac{sin(39.77^o)}{PR} \\\\\\ PR=\cfrac{20.8\cdot sin(39.77^o)}{sin(101^o)}\implies PR\approx 13.55`



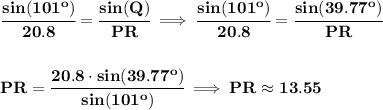
check the bottom part of the picture below.

since we already know that the angle A is 39.63°, then the angle at C, namely ACB will just be 180 - A - B, or about 49.37°.

and to get the length of AB,


`\bf \cfrac{sin(91^o)}{11.6}=\cfrac{sin(C)}{AB}\implies \cfrac{sin(91^o)}{11.6}=\cfrac{sin(49.37^o)}{AB} \\\\\\ AB=\cfrac{11.6\cdot sin(49.37^o)}{sin(91^o)}\implies AB\approx 8.80`