Question

Find a focus for this conic section. 9x^2+25y^2-200y+175=0

Answer 1

First of all we have to figure out what type of a conic this is. We know it's not a parabola because it has both an x-squared term and a y-squared term. There's a plus sign separating the squared terms so we know it also cannot be a hyperbola. It's either a circle or an ellipse. If this was simply a circle, though, we would not have leading coefficients on the squared terms (other than a 1). Circles have a standard form of
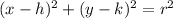
`(x-h)^2+(y-k)^2=r^2`. That makes this an ellipse. Let's group together the x terms and the y terms and move the constant over and complete the squares to see what we have.
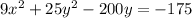
`9x^2+25y^2-200y=-175`. Since there's only 1 term with the x squared expression we cannot complete the square on the x's but we can on the y terms. First, though, the rule for completing the square is that the leading coefficient has to be a 1 and ours is a 25, so let's factor it out.
`9x^2+25(y^2-8y)=-175`. To complete the square we take half the linear term, square it, and add it to both sides. Our linear term is 8. Half of 8 is 4, and 4 squared is 16. So we add a 16 into the parenthesis, BUT we cannot disregard that 26 sitting out front there. It refuses to be ignored. It is still considered a multiplier. So what we are really adding on to the right side is 25*16 which is 400.
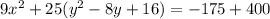
`9x^2+25(y^2-8y+16)=-175+400` which simplifies to
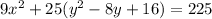
`9x^2+25(y^2-8y+16)=225`. The standard form of an ellipse is
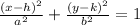
`((x-h)^2)/(a^2)+ ((y-k)^2)/(b^2) =1` if its horizontal axis is the transverse axis, or
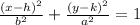
`((x-h)^2)/(b^2)+ ((y-k)^2)/(a^2)=1` if its vertical axis is the transverse axis. Notice that the a and b moved as the difference between the 2 equations. A is always the larger value and dictates which ellipse you have, horizontal or vertical. Our equation has a 225 on the right, so we will divide both sides by 225 to get that much-needed 1 on the right:
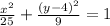
`(x^2)/(25)+ ((y-4)^2)/(9)=1`. Because 25 is larger than 9, this is a horizontal ellipse, our a value is the square root of 25 which is 5, and our b value is the square root of 9 which is 3. The center is (0, 4). You want the focus and now we can find it. The formula for the focus is
`c^2=a^2-b^2` where c is the distance from the center to the focus. We have an a and a b to find c:
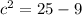
`c^2=25-9`, which gives us that c=4. The focus is 4 units from the center and always lies on the transverse axis. It shares a y value with the center and moves from the x-coordinate of the center the value of c. Our center is (0, 4) so our y value of the focus is 4; our x coordinate of the center is 0, so the x value of the focus is 4. The coordinates of the focus are (4, 4).