Question

Find the least common denominator for these two rational expressions.

Answer 1

The least common denominator of both the rational expression = (s-5)(s+5)(s + 1)

Explanation:

The rational expressions are:

`(s)/(s^2 - 25) ; (4s)/(s^2 - 4s - 5)`

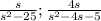
Now let's factorize the denominators.

`s^2 - 25 = s^2 - 5^2 = (s -5)(s +5)`

`s^2 -4s - 5 = s^2 -5s + s - 5`

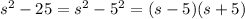
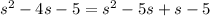
Now we have to group the terms and find the common factor.

`s^2 -5s + s - 5 = s(s -5) +1(s -5) = (s -5)(s +1)`

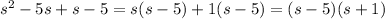
Now we have to find the least common denominator of the fractions.

To find the least common denominator, we have to take the common factors and missing factors, then we have to combine them to get the least common factor.

The common factor of both the denominators = (s -5)

Missing factor in the first rational expression = (s + 5)

Missing factor in the second rational expression = (s + 1)

Therefore, the least common denominator of both the rational expression = (s-5)(s+5)(s + 1)