Question

Q # 2 please help to solve

Answer 1

For this case, the first thing we must do is define variables.
We have then:
w: width
l: long
We write the perimeter of the garden:

`P = 2w + 2l = 376`
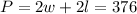
Then, the garden area is:

`A = w * l`
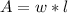
Writing the area depending on the width we have:

`A (w) = w * ((1/2) * (376 - 2w))`
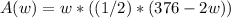
Rewriting we have:

`A (w) = (1/2) * (376w - 2w ^ 2)`
Deriving the area we have:

`A '(w) = (1/2) * (376 - 4w)`
We equal zero and clear w:

`(1/2) * (376 - 4w) = 0 376 = 4w w = 376/4 w = 94 feet`
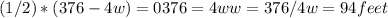
Then, the length is:

`l = (1/2) * (376 - 2w) l = (1/2) * (376 - 2 (94)) l = 94 feet`
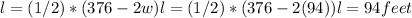
Finally, the area is given by:

`A = w * l A = 94 * 94 A = 8836 feet ^ 2`
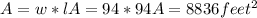Answer:
94 * 94; 8836
option 3

Answer 2

A rectangle with the greatest area is actually a square, with both the length and the width the same dimension.


The answer would be C. 94 x 94, 8836 ft.