Question

The options are 0.106,0.63,0.51,0.53

Answer 1

Call
`n` the number of responses.


`P(n \ \textless \ = 2) = P(n=0) + P(n=1) + P(n=2)`

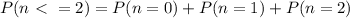
Each of those probabilities will be the frequency of occurrence of the particular event. We get zero responses 20 out of 200 times, 1 response 30 out of 200, and 2 responses 56 out of 200 times. So


`P(n \le 2) = (20)/(200) + (30)/(200) + (56)/(200) = (20+30+56)/(200) = (106)/(200) = 53\%`

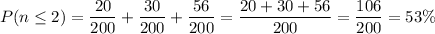
We see we could have just said 20+30+56=106 of the 200 editorials got zero, one or two responses, so the probability is 106/200.

Answer 2

That would be  (20+30+56)/200  =   106/200   = 53/100 Answer