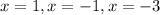Question

If f(1) = 0, what are all the roots of the function f(x)=x^3+3x^2-x-3? Use the Remainder Theorem.

Answer 1

I think you got it backwards! Its X=-3, X=-1, or X=1. So the answer is B. (2nd option) Well, you got it! ;)

Answer 2

There's no if about it,


`f(x)=x^3+3x^2-x-3`

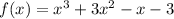
has a zero
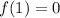
`f(1)=0` so
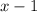
`x-1` is a factor. That's the special case of the Remainder Theorem; since
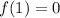
`f(1)=0` we'll get a remainder of zero when we divide
`f(x)` by
`x-1.`

At this point we can just divide or we can try more little numbers in the function. It doesn't take too long to discover
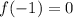
`f(-1)=0` too, so
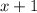
`x+1` is a factor too by the remainder theorem. I can find the third zero as well; but let's say that's out of range for most folks.

So far we have


`x^3+3x^2-x-3 = (x-1)(x+1)(x-r)`

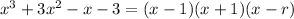
where
`r` is the zero we haven't guessed yet. Again we could divide
`f(x)` by
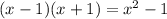
`(x-1)(x+1)=x^2-1` but just looking at the constant term we must have


`-3 = -1 (1)(-r) = r`

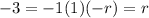
so


`x^3+3x^2-x-3 = (x-1)(x+1)(x+3)`

We check
`f(-3)=(-3)^3+3(-3)^2 -(-3)-3 = 0 \quad\checkmark`

We usually talk about the zeros of a function and the roots of an equation; here we have a function
`f(x)` whose zeros are


`x=1, x=-1, x=-3`