Completing the square is a way of factoring, and it is also a way to put a quadratic into vertex form to determine the vertex of the parabola. To begin completing the square, set the equation equal to 0 and then move the constant over by subtraction to get
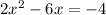 . The rule for completing the square is that the leading coefficient has to be a 1. Ours is a 2. So we have to factor it out.
. The rule for completing the square is that the leading coefficient has to be a 1. Ours is a 2. So we have to factor it out.
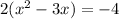 . We will take half the linear term, square it, and add it to both sides. Our linear term is 3. Half of 3 is 3/2 and 3/2 squared is 9/4. We add 9/4 inside the parenthesis. But outside is the 2 we factored out, hanging out front there, refusing to be ignored. It is a multiplier. That means what we have actually added in is 2*9/4 which is 18/4. That looks like this:
. We will take half the linear term, square it, and add it to both sides. Our linear term is 3. Half of 3 is 3/2 and 3/2 squared is 9/4. We add 9/4 inside the parenthesis. But outside is the 2 we factored out, hanging out front there, refusing to be ignored. It is a multiplier. That means what we have actually added in is 2*9/4 which is 18/4. That looks like this:
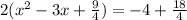 . On the right we will do the addition there by finding a common denominator, but on the left we have, in this process, created a perfect square binomial, the whole point of this nightmare. That looks like this:
. On the right we will do the addition there by finding a common denominator, but on the left we have, in this process, created a perfect square binomial, the whole point of this nightmare. That looks like this:
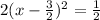 . The only left to do, if you need to, is move the 1/2 back over to the other side of the equals sign and set the quadratic back equal to y.
. The only left to do, if you need to, is move the 1/2 back over to the other side of the equals sign and set the quadratic back equal to y.
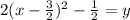 . The vertex of our parabola is (3/2, -1/2).
. The vertex of our parabola is (3/2, -1/2).