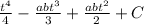Question

Calculate the indefinite integral : (assume t > a and t >

b. use c for the constant of integration.) t (t −a) (t −
b.dt

Answer 1

So here's your problem:
`\int\limits {[t(t-a)(t-b)]} \, dt`. The easiest way to do this is to distribute that whole thing out by FOIL-ing to get
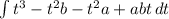
`\int\limits {t^3-t^2b-t^2a+abt} \, dt`. Now the integration is straightforward. We are integrating with respect to t, so treat a and b like "regular" numbers. Your integration, before simplifying, is
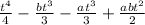
`(t^4)/(4)- (bt^3)/(3)- (at^3)/(3)+ (abt^2)/(2)`. Those 2 terms in the middle have the same denominator and power on the t, so we will combine those as like to get
`(t^4)/(4)- (abt^3)/(3)+ (abt^2)/(2)+C`