Triangles ABC and CDE and similar with ABC being dilated larger. This means we can use ratios to help solve for x, and then solve fo AC.
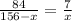
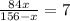
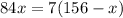
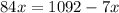
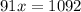
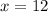
So, from this problem we now know that x is equal to 12. We merely need to plug that into what is given for AC and solve for AC.
AC = 156 - 12
AC = 144
Therefore, A is equal to 144.