Question

What is the slope of line A help ASAP

Answer 1

Hello!

The slope is
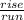
`(rise)/(run)`. One way we could do this is find two points on the line and form a right triangle to connect the two. We then divide the rise of this triangle by the run.

We can see the points (-3,-2) and (0,-1). As you can see, our rise is 1, and the run is 3. If we divide our rise by run, we get the slope of 1/3.
------------------------------------------------------------
The work we did above can be represented in the following formula.


`( y_(2) - y_(1) )/( x_(2)- x_(1) )`

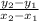
The ones and twos just represent a certain ordered pair. We will have (0,-1) be (
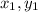
`x_(1) , y_(1)`) and (-3,-2) be (
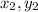
`x_(2) , y_(2)`). Now we plug our numbers into the formula. Note that the ones and twos can be swapped and the slope will be the same.


`(-2+1)/(-3-0) = (-1)/(-3) = (1)/(3)`

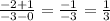
This proves that our slope is 1/3.

I hope this helps!

Answer 2

The slope of line A is m= 1/3