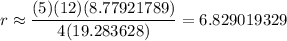Question

If AC=5cm, BC=12cm, and m AC= 40 degrees what is the radius of the circumscribed circle

Answer 1

Let's assume they meant C=40 degrees. With an angle like that they're asking for approximation; we'll oblige.

The circumradius is the product of the triangle sides divided by four times the area.

Here we have remaining side given by the Law of Cosines.


`AB^2 = AC^2 + BC^2 - 2\ AC \ BC \cos C`


`AB^2 = AC^2 + BC^2 - 2 AC \ AB \cos C = 5^2 + 12^2 - 2(5)(12) \cos 40^\circ`


`AB = √( 169 - 120 \cos 40 ^\circ) \approx 8.77921789`

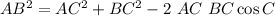
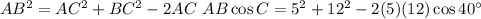
The area is
`\frac 1 2\ AC \ BC \sin C = \frac 1 2 (5)(12) \sin 40^\circ \approx 19.283628`



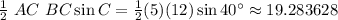
The circumradius is
`r \approx ((5)(12)(8.77921789 ))/( 4 (19.283628) ) = 6.829019329`