Question

If dy/dx equals xy squared and if y = 1 when x = 0, then when y = 3, x is equal to?

a) 1/8
b) - pi/8
c) 1
d) 2 square root 3 / 3

Answer 1

`\displaystyle (dy)/(dx)=xy^2\\ dy=xy^2 \, dx\\ (1)/(y^2)\, dy=x\, dx\\ \int (1)/(y^2)\, dy=\int x\, dx\\ -(1)/(y)=(x^2)/(2)+C\\\\ -(1)/(1)=(0^2)/(2)+C\\ C=-1\\\\-(1)/(3)=(x^2)/(2)-1\\ -2=3x^2-6\\ 3x^2=4\\ x^2=(4)/(3)\\ x=\sqrt{(4)/(3)} \vee x=-\sqrt{(4)/(3)}\\ x=(2)/(\sqrt3) \vee x=-(2)/(\sqrt3)\\ x=(2\sqrt3)/(3) \vee x=-(2\sqrt3)/(3)`

Answer 2

This is a separable differential equation, so let's start of there. Let's separate the variables to their own side with the respective differentials:

`(dy)/(dx) = xy^2`

`dy = (xy^2) dx`

`(1)/(y^2) dy = x dx`

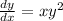
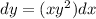
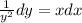
Let's integrate both sides (it's separable, so we can do this):

`\int\ { (1)/(y^2) } \, dy = \int\ {x} \, dx`

`- (1)/(y) = (x^2)/(2) + C`

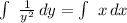
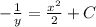
Now, let's plug in the values we are given to find the constant "C":

`- (1)/(1) =(0^2)/(2)+C`

`-1 = C`

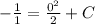
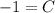
Let's rewrite the equation, with C in it, then solve for x because we need to ultimately find x:

`- (1)/(y) = (x^2)/(2) - 1`

`x = \sqrt{2(- (1)/(y)+1)}`

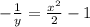
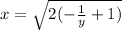
Let's plug in y = 3 and solve for x:

`x = \sqrt{2(- (1)/(3)+1)} = \sqrt{ 2( (2)/(3)) } = \sqrt{ (4)/(3) }`

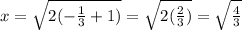
Let's simplify and rationalize the denominator:

`x = \sqrt{ (4)/(3)} = 2 \sqrt{ (1)/(3)} = 2 ( √(3) )/(3)`

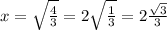
So, your answer is D.