Best thing to do with this is to FOIL it out to a third degree polynomial then integrate it term by term. In standard form the polynomial is
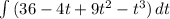
. We will use C as our constant of integration. The integral now, assuming you know the rules for exponents, is
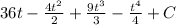
. Simplifying that we would get
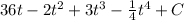
. There you go!