Question

Jack and Walter work in a store's gift-wrapping department. Jack can wrap 28 boxes in 2 hours, while Walter takes 3 hours to wrap 36 boxes of the same size. One day they work together for t hours to gift wrap 65 boxes. Which equation models this situation?

Answer 1

Hello!

First of all, we can simplify these ratios into 14:1 and 12:1. We will multiply these ratios into an equation.

\frac{14}{1} + \frac{12}{1} = \frac{26}{1} [/tex]

This shows that it would take them one hour to wrap 26 boxes. Our final proportion is shown below.


`(boxes)/(hours) = (26)/(1) = (65)/(t)`

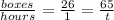
I hope this helps!

Answer 2

To solve this problem, we first need to find each of their hourly rates. We can do this by dividing the boxes by the number of hours. Using this method, we get that Jack wraps 14 boxes per hour and Walter wraps 12 boxes per hour. So, since the question has them working together, the rate is the sum of each of their individual rates per hour. Since we know that they work for t hours, we can multiply their combined rate by t (since in a job problem, job = time * rate). And, on the other end of the equal sign, since we know that they wrapped 65 presents, we put 65 there. The equation becomes:

(14+12)t = 65

Which simplifies to
26t = 65