This question is far easier to understand if we draw it out. I've included an image attachment to help show the relationships of the measurements. As we can see from the image, their positioning helps form a triangle that we can use the Pythagorean Theorem to find the connection range.
The Theorem is
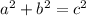
where a and b are the legs and c is the hypotenuse.
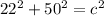
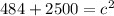
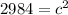
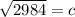

So the answer to the nearest meter is 55 meters.