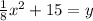Question

Someone help me please!!!!!!!!!!!

Answer 1

You have 3 unknowns: a, b, and c. That means you have to have 3 equations to solve for the values of them. 3 unknowns needs 3 different equations. We will use the first 3 points in the table and thank God that one of them has an x value of 0. We will replace the x and y in the general form of the quadratic with the x and y from the table, 3 times, to find each variable. Watch how it works. We will start with (0, 15).
`a(0)^2+b(0)+c=15`. That gives us right away that c = 15. We will do the same thing again with the second value in the table along with the fact that c = 15 to get an equation in a and b.
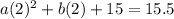
`a(2)^2+b(2)+15=15.5` which simplifies to 4a+2b=.5. Now do the same for the third set of coordinates from the table.
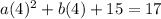
`a(4)^2+b(4)+15=17` which simplifies down to 16a+4b=2. Solve those simultaneously. Multiply the first bolded equation by -4 and then add that one to the second bolded one.
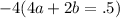
`-4(4a+2b=.5)` gives us -16a-8b=-2. Add that to the second bolded equation and the a terms cancel out giving us -4b=0 so b = 0. Subbing that back in we solve for a: 16a+4(0)=2 and 16a = 2. Therefore, a = 1/8. The quadratic then is
`(1)/(8)x^2+15=y`