Question

What is the solution to the linear absolute value equation 4|2x - 6| + 3 = 19? * 1 point a. x = -1 or x = -5 b. x = -1 or x = 5 c. x = 1 or x = 5 d. x = 1 or x = -5

Answer 1

You can find the solutions by graphing y = 4|2x -6| + 3 into
`Y_(1)` and
y = 19 into
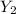
`Y_(2)`, and then find the intersections.

The intersections are x = 1 and x = 5.

Now, lets check it! It's always good to check your answers. :)

x = 1, 4|2x - 6| + 3 = 19
4|2(1) - 6| + 3 = 19
4|2 - 6| + 3 = 19
|8 - 24| + 3 = 19
|-16| + 3 = 19
16 + 3 = 19
19 = 19 It works!

4|2(5) - 6| + 3 = 19
4|10 - 6| + 3 = 19
|40 - 24| + 3 = 19
|16| + 3 = 19
16 + 3 = 19
19 = 19

Therefore, x = 1 and x = 5 which is c. :)