Question

Which of the following sets of numbers is a Pythagorean triple? help i begg of YOU!!!!

77, 35, 112
70, 35, 78
75, 36, 83
77, 36, 85

Answer 1

One way to find the answer is to add the squares of the smaller numbers, and see that the sum equals the square of the largest number.
Example:
77^2+35^2=5929+1225=7154
112^2=12544
So the first triplet is not Pythagorean.
Repeat for the other triplets to find the answer.

Another way is to first eliminate the impossible (triplet=(a,b,c), a<c, b<c)
- if a+b>=c, then triplet is not Pythagorean
77+34=112, ==> (77,34,112) is not Pythagorean
- check the last digits. if the last digit of the sum of the squares of the last digits of the smaller number is not equal to the last digit of the square of the largest number, the triplet is not Pythagorean
Example: For (70,35,78),
0^2+5^2=0+25 last digit is 5.
8^2=64 last digit is 4 4 &ne; 5 => triplet is not pythagorean.
(75,36,83) : 5^2+6^2=25+36=61 => last digit is 1 3^2=9
1 &ne; 9, so (75,36,83) is not Pythatorean.

Since we have eliminated the first three triplets, we have no choice but to check the squares of the last triplet:
77^2=5929
36^2=1296
Sum=5929+1296=7225
85^2=7225 = 77^2+36^2 => (77,36,85) is a Pythagorean triplet

Answer 2

Hey!


Now, to find the Pythagorean triple we must first start off by finding the quare of the two smallest numbers in the data set. After we find the square of both of them, we will then add them together. If our product does not equal the square of our remaining number in the data set, then it is not a Pythagorean triple. If it does, then it is a Pythagorean triple.

So, let's start with the first set of numbers. Since the smallest numbers in the first number set are 77 and 35, we'll start by find the square of those.

Square of
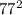
`77^(2)` - 5,929

Square of
`35^(2)` - 1,225

And now we add those together.

5,929 + 1,225 = 7154

And now to determine that this it is a Pythagorean triple we'll find the square of the remaining number in our data set and if it DOES equal the same as our product then it is a Pythagorean triple.


`112^(2)` - 12,544

7154
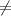
`\\eq` 12544

So, since these do not equal this is not a Pythagorean triple.

We'll do the same for the next three sets.

SET #2


`70^(2)` - 4900


`35^(2)` - 1225

4900 + 1225 = 6125


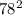
`78^(2)` - 6084

6125
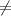
`\\eq` 6084

Not equal so this is not a Pythagorean triple.

SET #3


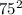
`75^(2)` - 5625


`36^(2)` - 1296

5625 + 1296 = 6921


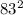
`83^(2)` - 6889

6921
`\\eq` 6889

Not equal so this is not a Pythagorean triple.

SET #4


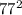
`77^2` - 5929


`36^(2)` - 1296

5929 + 1296 = 7225


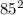
`85^(2)` - 7225

7225 = 7225

These numbers are equal.

So, this means that the last set is a Pythagorean triple.

Hope this helps!


- Lindsey Frazier ♥