2 Answers

IDelusion · Answer 1 · 2019-07-01T04:46:22+0000

Answer:

The parabola opens to the right

Explanation:

The given equation corresponds to a parabola.

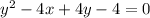
y^(2) -4x + 4y - 4 = 0

We can rewrite this formula in vertex form (
x = a(y - y_(0))^(2) + x_(0) ) to be able to locate the vertex and its direction

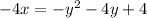-4x = -y^(2) - 4y + 4 (isolate 4x on the left)

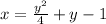$x = \frac{y^(2)} {4} + y - 1$ (divide both sides by -4)

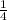$x = \frac{1} {4} (y^(2) + 4y) - 1$ (common factor
$\frac{1} {4}$ between
$\frac{y^(2)} {4}$ and
)

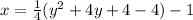$x = \frac{1} {4}(y^(2) + 4y + 4 - 4) - 1$ (add and substract 4 to complete square)

$x = \frac{1} {4}(y^(2) + 4y + 4) - 4 - 1$ (associate to get square inside parentheses)

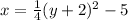$x = \frac{1} {4}(y + 2)^(2) - 5$ (collapse square inside parentheses)

We can conclude the following:

- Its vertex is (-5, -2)

- Its axis of symmetry is y = -2

- Coefficient a = 1/4 is positive

The parabola opens to the right (see the attachment)

Please log in or register to add a comment.