Question

What is the sum of the geometric series 3∑i=1(8(1/4)^i-1)?

A.) 21
B.) 21/2
C.) 10
D.) 21/8

Answer 1

The answer should be b

Answer 2

`(21)/(2)`

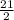
Explanation:

Geometric series is a sequence of form
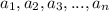`a_1,a_2,a_3,...,a_n`, such that
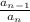`(a_(n-1))/(a_(n))` is constant .

To find : sum of the geometric series
`\sum_(i=1)^(3)\left ( 8\left ( (1)/(4) \right )^(i-1) \right )`

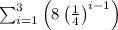
Solution:

For i = 1:

Put i = 1 in the term
`8\left ( (1)/(4) \right )^(i-1)`

`\left ( 8\left ( (1)/(4) \right )^(i-1) \right )=\left ( 8\left ( (1)/(4) \right )^(1-1) \right )=8(1)=8`

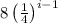
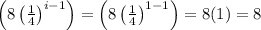
( here, formula used:
`a^0=1` )

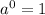For i = 2:

Put i= 2 in the term
`8\left ( (1)/(4) \right )^(i-1)`

`\left ( 8\left ( (1)/(4) \right )^(i-1) \right )=\left ( 8\left ( (1)/(4) \right )^(2-1) \right )=(8)/(4)=2`

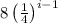
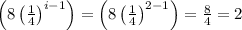
For i = 3:

Put i = 3 in the term
`8\left ( (1)/(4) \right )^(i-1)`

`\left ( 8\left ( (1)/(4) \right )^(i-1) \right )=\left ( 8\left ( (1)/(4) \right )^(3-1) \right )=(8)/(16)=(1)/(2)`

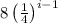
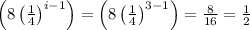
Therefore,

`\sum_(i=1)^(3)\left ( 8\left ( (1)/(4) \right )^(i-1) \right )=\left ( 8\left ( (1)/(4) \right )^(1-1) \right )+\left ( 8\left ( (1)/(4) \right )^(2-1) \right )+\left ( 8\left ( (1)/(4) \right )^(3-1) \right )\\=8+2+(1)/(2)\\=(16+4+1)/(2)\\=(21)/(2)`

So, option 2. is correct