Question

Two trains leave the station at the same time, one heading east and the other west. The eastbound train travels 16 miles per hour faster than the westbound train. If the two trains are 800 miles apart after 4 hours, what is the rate of the eastbound train? Do not do any rounding.

Answer 1

We'll use variables to represent the speeds of the eastbound and westbound trains.

x will represent the speed of the eastbound train.
y will represent the speed of the westbound train.

The eastbound train is 16 mph faster than the westbound train. An equation can be made from this:


`x - y = 16`

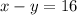
Subtraction is used, because it represents the difference in distances between the two trains if they travel the same direction.

After 4 hours, the trains are 800 miles apart. An equation can be made from this:


`4x + 4y = 800`

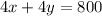
Addition is used, because the trains are heading in opposite directions, which means their distances from the starting point are added together.

Set the two equations up vertically:


`x - y = 16`

`4x + 4y = 800`

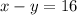
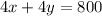
We will use elimination to solve for x.

Multiply the entire first equation by 4 so that the coefficients for y will be opposite numbers:


`(x - y = 16) * 4 = 4x - 4y = 64`


`4x - 4y = 64`

`4x + 4y = 800`

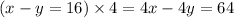
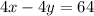
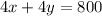
Combine the two equations together to cancel out y:


`8x = 864`

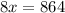
Divide both sides by 8 to get x by itself:


`x = 108`

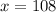
The speed of the eastbound train is 108 mph.