To figure out the point where the second car will overtake the first car, we must create equations that equal each other.
The first car goes 50 km/h. The second car goes 70km/h, but it reaches the landmark an hour after the first car. The following equation can be set up from this information:
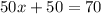
x represents the time it takes for the cars to meet each other after passing the landmark. We add 50 to the left side (first car), because that is the distance between the two cars when the second car reaches the landmark an hour later.
Subtract 50x from both sides:

Divide both sides by 20 to get x by itself:

The second car will overtake the first car
2.5 hours after passing the landmark.