Question

What set of reflections would carry parallelogram ABCD onto itself?

Parallelogram ABCD is shown. A is at negative 1, negative 2. B is at negative 2, negative 1. C is at negative 4, negative 1. D is at negative 3, negative 2.

Answer Choices

x-axis, y=x, x-axis, y=x

y=x, x-axis, y=x, y-axis

y-axis, x-axis, y-axis

x-axis, y-axis, y-axis

Answer 1

Choice B is the correct answer

Answer 2

The correct option is 2.

Explanation:

The vertices of parallelogram ABCD are A(-1,-2), B(-2,-1), C(-4,-1), D(-3,-2).

In option 1, ABCD reflected about x-axis, y=x, x-axis, y=x.

`(x,y)\rightarrow(x,-y)\rightarrow(-y,x)\rightarrow(-y,-x)\rightarrow(-x,-y)\\eq(x,y)`

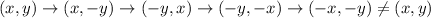
Therefore option 1 is incorrect.

In option 2, ABCD reflected about y=x, x-axis, y=x, y-axis.

`(x,y)\rightarrow(y,x)\rightarrow(y,-x)\rightarrow(-x,y)\rightarrow(x,y)=(x,y)`

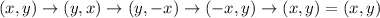
Therefore the parallelogram ABCD onto itself. Option 2 is correct.

In option 3, ABCD reflected about y-axis, x-axis, y-axis.

`(x,y)\rightarrow(-x,y)\rightarrow(-x,-y)\rightarrow(x,-y)\\eq (x,y)`

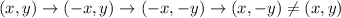
Therefore option 3 is incorrect.

In option 4, ABCD reflected about x-axis, y-axis, y-axis.

`(x,y)\rightarrow(x,-y)\rightarrow(-x,-y)\rightarrow(x,-y)\\eq (x,y)`

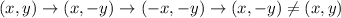
Therefore option 4 is incorrect.