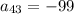This is an arithmetic sequence. The first term,
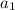
, is 27. The common difference is -3 (you subtract 3 from a number to get to the next number in line), and you are looking for term number 43, or
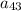
. Your formula for an arithmetic sequence is
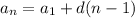
. If we are looking for term number 43, our first number in the sequence is 27, and the common difference is -3, then our formula is this one:

, which simplifies to
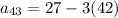
, which is
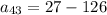
and