Question

You are a research scientist studying bioluminescent bacteria (bacteria that can glow). You grow several plates of bacteria and give them a special chemical that you hypothesize will increase their luminescence, or brightness. You turn off the lights and use a device called a photometer to measure the light levels (in lumens) coming from each plate. You collect the following data:

Plate 1: 7 lumens, 6 lumens, 13 lumens
Plate 2: 4 lumens, 5 lumens, 7 lumens
Plate 3: 3 lumens, 6 lumens, 7 lumens
Plate 4: 5 lumens, 5 lumens, 8 lumens
Which of the following pieces of data is likely an outlier?
A. Plate 2, trial 1
B. Plate 3, trial 1
C. Plate 1, trial 3
D. Plate 4, trial 2

Answer 1

C. Plate1, Trial 3

Step-by-step explanation:

In a given data set, outliers are data points that lie very much above or way below the other values. Presence of outliers can skew a data set and can result in erroneous values for mean and standard deviation.

An outlier can be identified if its value is lower than:
`Q1-1.5(IQR) -----(1)</strong>`

or if it is higher than:
`Q3+1.5(IQR) -----(1)`

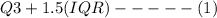
where Q1 = first quartile, Q3 = third quartile

IQR = interquartile range i.e. Q3-Q1

In the given example, consolidating the data from plate 1, 2, 3 and 4 as well as trials 1,2 and 3 gives a data set with essentially 12 values for the light intensity measured in lumens:

Data set showing the measured lumens:

3,4,5,5,5,6,6,7,7,7,8,13

The data set of 12 points can be divided into 2 halves:

3,4,5,5,5,6 and 6,7,7,7,8,13

The first quartile is the median of the upper half: Q1 =
`(5+5)/(2) = 5`

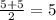
The third quartile is the median of the lower half: Q3 =
`(7+7)/(2) = 7`

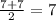
IQR = Q3-Q1 = 7-5 = 2

Based on equation (1):
`5-1.5(2) = 2`

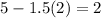
Based on equation(2):
`7+1.5(2) = 10`

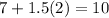
Therefore, any point that is lower than 2 or higher than 10 is an outlier. In the given data set, there are no numbers lower than 2 however there is one value higher than 10. Hence, 13 is an outlier which is a data point in Plate 1, Trial 3.

Answer 2

The answer is C. Outliers are data points that fall way off the average range of values in a dataset. In this case, the number 13 is way off from the rest of the values which range between 4 and 7. An outlier may represent an error in an experiment that involved many treatments.