Question

Find the inverse of the given function.

f(x) = -1/2√x + 3, x ≥ -3

Answer 1

The inverse of the function is
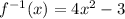`f^(-1)(x)=4x^2-3`, for
`x\leq 0`

Explanation:

Given : Function
`f(x)=-(1)/(2)√(x+3)`

To find : The inverse of the given function?

Solution :

To find the inverse of the function we replace the value of x and y and then find y in terms of x which is the inverse of the function.

Let f(x)=y

`y=-(1)/(2)√(x+3)`

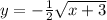
Replace the value of x and y.

`x=-(1)/(2)√(y+3)`

Now, we solve in terms of x the value of y

`-2x=√(y+3)`

(x must be negative)

Squaring both side,

`(-2x)^2=(√(y+3))^2`

`4x^2=y+3`

`4x^2-3=y`

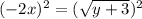
So, The inverse of the function is
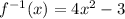`f^(-1)(x)=4x^2-3`, for
`x\leq 0`