Answer:
The length of missing side of triangle is 10 m.
Step-by-step explanation:
Solution :
Here, we have given that the two sides of triangle are 6 m and 8 m.
Finding the third side of triangle by pythagorean theorem formula :
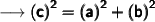
Substituting all the given values in the formula to find the third side of triangle :
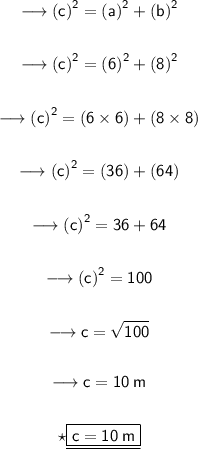
Hence, the length of missing side of triangle is 10 m.
