Question

PLEASE HELP ASAP!!!

Graph the data in the table. Which kind of function best model the data? write an equation to model the data

A. linear; y = 2x

B. Quadratic; y = 2x^2

C. Exponential; y = 2 · 2^x

D. Exponential; y = 4 · 2^x

Answer 1

can you help me after Clairebear? I really need help with a question I just posted. It is for my exam.

Answer 2

Looking at the possible answers, the only one that fits is D.

Let's first look at A: y = 2x
We know this doesn't work, since if you plug in 0 for x, y = 0, not 4.

Let's look at B: 2x^2
We know this doesn't work either, since if x is 0, y = 0, not 4.

Let's look at C: 2 × 2^x
We know this doesn't work, since if x = 0, y = 2:

`y = 2 * {2}^(x) \\ 4 = 2 * {2}^(0) \\ 4 = 2 * 1 \\ 4 = 2`
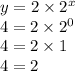
This leaves D: 4 × 2^x:

`y = 4 * {2}^(x) \\ 4 = 4 * {2}^(0) \\ 4 = 4 * 1 \\ 4 = 4`
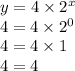
It also works for (1,8) and (2,16):

`y = 4 * {2}^(x) \\ 8 = 4 * {2}^(1) \\ 8 = 4 * 2 \\ 8 = 8`


`y = 4 * {2}^(x) \\ 16 = 4 * {2}^(2) \\ 16 = 4 * 4 \\ 16 = 16`
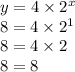
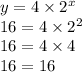
The answer is D.