Question

Which of the following equations represents a graph that increases the most rapidly?

Answer 1

I would imagine it would be the first one because the coefficient of 4 has the greatest effect out of all of them

Answer 2

A .
`y =4x^(2) +10x -6`

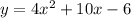
Explanation:

Here the degree of all equations (polynomial) are 2 but the leading coefficient of
`x^(2)` in all equation are different which are the following.

(1). The leading coefficient of
`x^(2)` in the equation
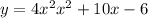`y =4x^(2) x^(2) +10x-6` is 4.

(2). The leading coefficient of
`x^(2)` in the equation
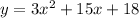`y =3x^(2)  +15x+18` is 3.

(3). The leading coefficient of
`x^(2)` in the equation
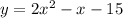`y =2x^(2) -x -15` is 2.

(4). The leading coefficient of
`x^(2)` in the equation
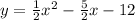`y= (1)/(2) x^(2) -(5)/(2) x-12` is 0.5.

In the above four equations the leading coefficient of
`x^(2)` is greatest in the equation
`y=4x^(2)  +10x-6` .

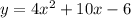Hence the graph of
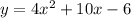`y =4x^(2) +10x -6`is increases most rapidly.