Question

What is a zero of the quadratic function f(x)=4x^2+24+11?

Answer 1

The roots of this equation are x = -5.5 and x = -.5

We can find this by using the quadratic equation which is listed below.

`\frac{-b +/- \sqrt{b^(2) -4ac}}{2a}`

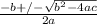
Now in order to find the right numbers to put into this equation. we look back to the original problem. Our a value will always be the number attached to x^2 (in this case 4), the b value will be attached to x (24) and the c value will be attached to no variable (11). Now we can do the operations and solve.

`\frac{-b +/- \sqrt{b^(2) -4ac}}{2a}`

`\frac{-24 +/- \sqrt{24^(2) -4(4)(11)}}{2(4)}`

`(-24 +/- √(488))/(8)`

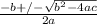
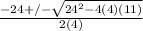
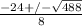
-3 +/- 5/2

-3 + 5/2 = -0.5 and -3 - 5/2 = -5.5

Giving you those x values.