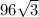Answer:
 inches
inches
Explanation:
Here we are going to use the formula which is
Area=
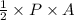
Where P is perimeter and A is apothem
Here we are given that the Perimeter is 48 inches: Where perimeter is givenas
P=6s
Where s is the side of the hexagon
6s=48
s=8 inches
Please refer to the image attached with this :
In a Hexagon , there are six equilateral triangle being formed by the three diagonals which meet at point O.
Consider one of them , 0PQ with side "s"
As Apothem is the Altitude from point of intersection of diagonals to one of the side. Hence it divides the side in two equal parts . hence
Also OP= s
Using Pythagoras theorem ,
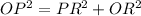
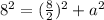
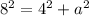

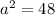
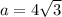
Hence We have Apothem
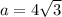
also we have the perimeter as 48
Now we put them in the main formula
Area =

Area=
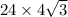
Area=