Question

Which statements about the graph of the function f(x) = –x2 – 4x + 2 are true? Check all that apply. The domain is x. The range is y ≤ 6. The function is increasing over the interval (–∞ , –2). The function is decreasing over the interval (−4, ∞). The function has a positive y-intercept.

Answer 1

The range is y ≤ 6

The function is increasing over the interval (–∞ , –2)

The function has a positive y-intercept

Answer 2

The graph of the function
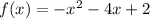
`f(x) =-x^2-4x + 2` is parabola with branches going down in the negative direction of y-axis.
The vertex of parabola has coordinates:


`x_v=(-(-4))/(2\cdot(-1))=-2, \\ y_v=-(-2)^2-4\cdot (-2)+2=-4+8+2=6`

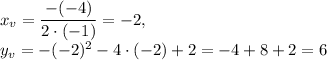
Then you can conclude that all x are possible, that means that the dimain is
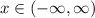
`x\in (-\infty,\infty)` and the maximum value of y is at the vertex, then the range is
`(-\infty,6]`.The function is increasing for x<-2 and decreasing for x>-2 (since vertex is the maximum point).
When x=0, y=2.
Hence,
The domain is x ≤ –2 - false.

The range is y - true.

The function is increasing over the interval (–∞ , –2) - true.

The function is decreasing over the interval (−4, ∞) - false.

The function has a positive y-intercept - true.