Given the table of points that lie on a parabola.
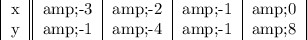
The equation of a parabola is given by
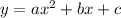
, where a, b and c are constants. Since the equation of a data point has three constants, three data points/equations will be needed to obtain the value of the constants and hence the required equation.
when x = 0, y = 8 and we have:

When x = -1, y = -1 and we have:
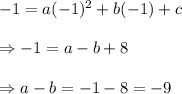
When x = -2, y = -4 and we have:
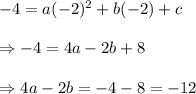
Solving the two equations simultaneously, we have:

Thus, a = 3, b = 12 and c = 8
Therefore, the required equation of the parabola is given by:
