Question

For the graphed function f(x) = (4)x − 1 + 2, calculate the average rate of change from x = 1 to x = 2.

graph of f ox x equals 4 to the x minus 1 power, plus 2

Answers =


−3

3

2

−2

Answer 1

Option B is correct.

Average rate of change from x=1 to x=2 is 3

Explanation:

Formula for Average rate of change: The ratio of the difference in the function f(x) as it changes from a to b to the difference between a and b :

`A(x) = (f(b)-f(a))/(b-a)`

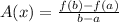
As per the statement:

`f(x) = 4^(x-1) +2`

Calculate the average rate of change from x =1 to x =2

At x = 1

`f(1) = 4^(1-1) +2 = 1 +2 = 3`

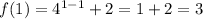
At x = 2

`f(2) = 4^(2-1) +2 = 4^1 +2 = 4+2 =6`

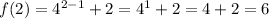
Then;

`A(x) = (f(2)-f(1))/(2-1) = (6-3)/(1) =(3)/(1) = 3`

Therefore, the average rate of change from x=1 to x=2 is 3

Answer 2

For the function
f(x) = 4^(x-1) +2
the average rate of change on the interval [1, 2] is found by computing
(f(2) - f(1))/(2 - 1)
= ((4^1+2) - (4^0+2)/1
= (6-3)
= 3