For this case we have a function of the form:

Where,
A: initial population
b: growth rate
x: time in hours
y: population after x hours
We must find the values of A and b, for this we use the following data:
After 1 hour, the population is 18:

After 2 hours, the population is 27:
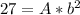
We have a system of two equations with two unknowns
Dividing equations we have:
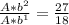
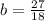
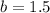
Substituting b in equation 1 we have:
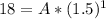
Clearing A we have:
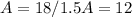
So, the function is:
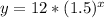
Answer:
A function that best describes the relationship between the time, in hours, and the population of the bacterium is:
C: EXPONENTIAL
the y-intercept of the function:
B: 12
the rate of change of the function:
C: MULTIPLY 1.5