Question

Hunter wants to build a sidewalk of uniform width around his pool. His pool is rectangular, and its dimensions are 60 feet by 40 feet. He has enough pavers to cover 1200 square feet and wants to use all the pavers. Complete the following statement. Round to the nearest tenth. Hunter should make the width of the sidewalk _____ feet.

Answer 1

let
x--------> the width of the sidewalk

we know that
Area of the sidewalk=[(60+2x)*(40+2x)]-[60*40]------> equation 1
Area of the sidewalk=1200 ft²------> equation 2

equate equation 1 and equation 2
[(60+2x)*(40+2x)]-[60*40]=1200
2400+120x+80x+4x²-2400=1200
4x²+200x-1200=0

using a graph tool------> to resolve the second order equation
see the attached figure

the solution is
x=5.414 ft--------> x=5.4 ft

the answer is
the width of the sidewalk is 5.4 ft

Answer 2

The width of the sidewalk should be 5.4 feet.

Explanation:

The dimension of his pool = 60 ft × 40 ft. So that the area of his pool = 2400
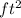`ft^(2)`. But he has enough pavers to cover 1200

Let the width of the sidewalk be represented by w. Thus,

(60 + 2w)(40+ 2w) - 60(40) = 1200

2400 + 120w + 80w + 4
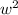`w^(2)` -2400 = 1200

2400 + 200w + 4
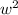`w^(2)` -2400 = 1200

4
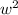`w^(2)` + 200w -1200 = 0

Divide through by 4, to have;

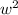`w^(2)` + 50w - 300 = 0

Solving the quadratic equation by formula, we have;

w = (-b ±
`\sqrt{b^(2) - 4ac}`) ÷ 2a

where from the equation; a = 1, b= 50 and c= -300. Substituting these in the expression gives,

w = (-50±
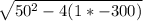`\sqrt{50^(2) -4(1*-300) }`) ÷ 2*1

w = (-50±60.8276) ÷ 2

w = (-50+60.8276) ÷ 2 or (-50-60.8276) ÷ 2

w =
`(10.8276)/(2)` or
`(-110.8276)/(2)`

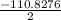
w = 5.4138 or -55.4138

w = 5.4138

Therefore, the width of the sidewalk should be 5.4 feet.