Question

The first three steps in determining the solution set of the system of equations algebraically are shown in the table. y = −x2 +2x − 9 y = −6x + 6 What are the solutions of this system of equations? (5, −24) and (3, −12) (5, 36) and (3, 24) (−5, −24) and (−3, 12) (−5, 36) and (−3, 24)

Answer 1

You have a system of equations
`\left \{ {{y = -x^2+2x-9} \atop {y =-6x+6}} \right.`.

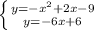
1. Substitude right side of second equation into the left side of the first equation:
`-6x+6=-x^2+2x-9`.

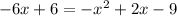
2. Solve this equation:

`x^2-2x+9-6x+6=0, \\ x^2-8x+15=0, \\ D=(-8)^2-4\cdot 1\cdot 15=64-60=4, \\ √(D)=2, \\ x_(1,2)=(8\pm 2)/(2 ) =3,5`.

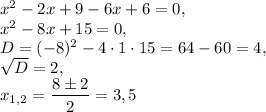
3. Find y:
for
`x_1=3, y_1=-6\cdot 3+6=-18+6=-12`,
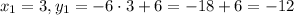
for
`x_2=5, y_2=-6\cdot 5+6=-30+6=-24`.

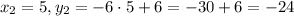
4. The solutions of the system are: (3,-12) and (5,-24).
Answer: Correct choice is A.