The graph shown above is a "parabola" and the parent function is x². So, we can start off at x². The graph of x² intersects the x and y-axis at (0, 0). In this case, it's simply being shifted up by 1 and intersects the x and y-axis at (0, 1). Therefore, the equation is:

To check, let's plug in 0 for x, and see what we get (we should get 1):

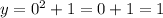
We are right, so your final answer is
x² + 1.