The first thing you need to do is distribute the 7 into the set of parenthesis on the right. That will give you

. Then add 3 to both sides:
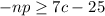
. Divide both sides by p to get
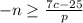
. Now divide both sides by -1. This is where the sign of inequality is going to change direction. That's why I saved it til last so we could make a point of making sure it gets done.
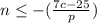
and if you distribute the negative in your solution is

. Or you could write the positive expression first, as many of us prefer:
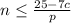
. There you go!