Question

George has 100 meters of fence. He wants to enclose a rectangular region for his dog making the area as large as possible. What is the maximum are he Can enclose Using 100 meters of fence?

Answer 1

Let x be the width of the fence and y be the length of the fence. Then the perimeter of the fence is x+x+y+y=100. You see that x+y=50 and y=50-x.

The area of the fence is A(x)=x·y=x(50-x),

`A(x)=50x-x^2`.

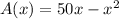
Find the derivative:

`A'(x)=50-2x \\ A'(x)=0 \Rightarrow 50-2x=0, \\ x=25`

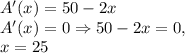
For x<25, A'(x)>0 and for x>25, A'(x)<0, this means that x=25 is the maximum point and A(25)=25·(50-25)=25·25=625 is the maximum area.

Answer: maximally he can enclose 625 sq. m area