Question

In △ABC, m∠A=19°, a=13, and b=14. Find c to the nearest tenth.

Answer 1

25.4

Explanation:

Answer 2

we know that
Applying the law of sines

step 1
Find the value of angle B
a=13
b=14
A=19°
so


`(a)/(sin A) = (b)/(sin B) \\ a*sin B=b*sin A \\ sin B= (b)/(a)*sin A \\ sin B= (14)/(13) *sin 19 \\ sin B=0.3506 \\ B=arc sin(0.3506) \\ B=20.5`°

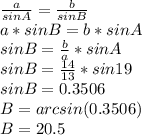
step 2
with angle A and angle B find the angle C
A+B+C=180-----> solve for C
C=180-(A+B)------> C=180-(19+20.5)-----> C=140.5°

step 3

`(a)/(sin A) = (c)/(sin C) \\ a*sin C=c*sin A \\ c=a* (sin C)/(sin A) \\ c=13* (sin 140.5)/(sin 19) \\ c=25.4`

the answer is
the value of c is 25.4