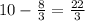Question

Use the method of quadrature to estimate the area under the curve y=-x^2+5 and above the x-axis from x=0 to x=2.

Answer 1

I'm a calculus teacher at the high school level and I have never heard of quadrature. I teach from an AP approved college-level text so...I'll do it using the antiderivative! Setting that up to integrate we have
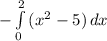
`- \int\limits^2_0 { (x^2-5)} \, dx`. If you notice, I pulled the negative out in front of the integral and changed the signs in the function. So it could really be rewritten as
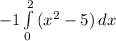
`-1 \int\limits^2_0 {(x^2-5)} \, dx`. Integrating we have
`-1[ (x^3)/(3) -5x]` from 0 to 2. Subbing in those bounds, we have
`-1[( (2^3)/(3)-5(2))-( (0^3)/(3)-5(0))]` which simplifies to
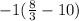
`-1( (8)/(3)-10)`. Distributing the -1 in gives us
`10- (8)/(3)= (22)/(3)`

Answer 2

Area =
`(22)/(3)`

Explanation:

Given is a curve

`y=-x^2+5`

we have to find the area of this curve above x axis from 0 to 2

By method of quadrature we know that area of a curve above x axis is given by,

`\int\limits^a_bf( {x} )\, dx`

Here a= 0 and b =2

Substitute to get

Area =
`\int\limits^0_2 {-x^2+5} \, dx \\=(-x^3)/(3) +5x`

Substituting limits

Area =
`(-8)/(3) +10 =(22)/(3)`