The max value can be found by setting the derivative equal to 0 and solving for x, then subbing that value for x back into the original function and solving for y.
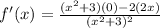
which simplifies to
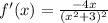
. This derivative is equal to 0 when -4x is equal to 0. If -4x = 0, then x = 0. If we find f(0), then
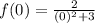
and y here is 2/3. So the max value occurs at (0, 2/3). There you go!