Question

A 15.0 m long steel rod expands when its temperature rises from 34.0 degrees C to 50.0 degrees C. What is the change in the beam's length due to the thermal expansion? Steel has a coefficient of linear expansion of 12.0 E -6/C degrees.

0.0612 m
0.00432 m
0.00288 m
0.0119 m
0.0475 m

Answer 1

0.00288................

Answer 2

The change in beam's length due to the thermal expansion is 0.00288 meters.

Step-by-step explanation:

Given that,

Original length of the steel rod, l = 15 m

Initial temperature,
`T_i=34^(\circ) C`

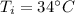
Final temperature,
`T_f=50^(\circ) C`

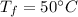
The coefficient of linear expansion of the steel,
`\alpha =12* 10^(-6)\ /^(\circ) C`

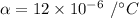
Let
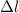`\Delta l` is the change in beam's length due to the thermal expansion. It can be given by :

`(\Delta l)/(l)=\alpha (T_f-T_i)\\\\\Delta l=l\alpha (T_f-T_i)\\\\\Delta l=15* 12* 10^(-6)* (50-34)\\\\\Delta l=0.00288\ m`

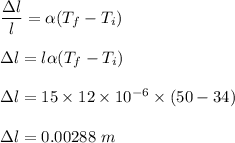
So, the change in beam's length due to the thermal expansion is 0.00288 meters. Hence, this is the required solution.